Tumbukan (Impuls dan Momentum)

Tumbukan 

 

Contoh peristiwa tumbukan

Dalam kehidupan ini, banyak kita jumpai peristiwa tumbukan. Tabrakan mobil di jalan raya, bus menabrak pohon, tumbukan dua bola biliar, tumbukan antara bola dengan tanah atau dinding merupakan contoh peristiwa tumbukan. Tumbukan dapat terjadi pada saat benda yang bergerak mengenai benda lain yang sedang bergerak atau diam. Pada materi ini, kita hanya akan membahas mengenai tumbukan sentral lurus, yaitu tumbukan antara dua benda yang arah kecepatannya berimpit dengan garis hubung kedua pusat massa benda.

Berdasarkan sifat kelentingan benda, tumbukan dibedakan menjadi tiga jenis, yaitu tumbukan lenting sempurna, tumbukan lenting sebagian, dan tumbukan tidak lenting sama sekali. Dengan menggunakan Hukum Kekekalan Momentum dan Hukum Kekekalan Energi, kita dapat menentukan peristiwa yang terjadi setelah tumbukan. 

1. Tumbukan Lenting Sempurna 

Apabila tidak ada energi yang hilang selama tumbukan dan jumlah energi kinetik kedua benda sebelum dan sesudah tumbukan sama, maka tumbukan itu disebut tumbukan lenting sempurna. Pada tumbukan lenting sempurna berlaku Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik. Misalnya, dua buah benda massanya masing-masing m₁ dan m₂ bergerak dengan kecepatan v₁ dan v₂ dengan arah berlawanan seperti pada gambar berikut.

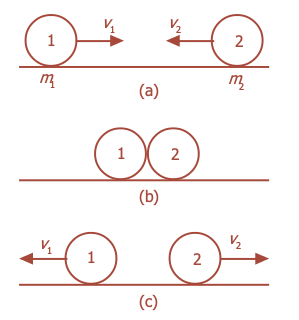
Tumbukan lenting sempurna antara dua benda: 

(a) sebelum tumbukan, (b) saat tumbukan, (c) setelah tumbukan.

Kedua benda bertumbukan lenting sempurna, sehingga setelah tumbukan kecepatan kedua benda menjadi v₁' dan v₂' . Berdasarkan Hukum Kekekalan Momentum, dituliskan:

m₁ v₁ + m₂ v₂ = m₁ v₁' + m₂ v₂'

m₁ v₁ – m₁ v₁' = m₂ v₂' – m₂ v₂

m₁ (v₁ – v₁' ) = m₂ (v₂' – v₂ )

(i)

Dari Hukum Kekekalan Energi Kinetik diperoleh:

(ii)

Jika persamaan (ii) dibagi dengan persamaan (i) diperoleh:

v₁ + v₁' = v₂' + v₂

v₁' – v₂' = v₂ – v₁

v₁' – v₂' = -(v₁ – v₂ )

 

(2)

Persamaan (2) dapat dituliskan:

(3)

Bilangan pada persamaan (3) disebut koefisien restitusi (e), yang merupakan negatif perbandingan kecepatan relatif kedua benda sebelum tumbukan. Persamaan (3) dapat dinyatakan:

(4)

Dengan demikian, pada tumbukan lenting sempurna koefisien restitusi (e) = 1.

2. Tumbukan Lenting Sebagian

Pada tumbukan lenting sebagian, beberapa energi kinetik akan diubah menjadi energi bentuk lain seperti panas, bunyi, dan sebagainya. Akibatnya, energi kinetik sebelum tumbukan lebih besar daripada energi kinetik sesudah tumbukan. Sebagian besar tumbukan yang terjadi antara dua benda merupakan tumbukan lenting sebagian.

Pada tumbukan lenting sebagian berlaku Hukum Kekekalan Momentum, tetapi tidak berlaku Hukum Kekekalan Energi Kinetik.

ΣEk > ΣEk ' , maka:

Ek₁ + Ek₂ > Ek₁' + Ek₂'

v₂ – v₁ > v₁' – v₂'

Sehingga persamaan (3) dapat dituliskan:

(5)

Dengan demikian, dapat disimpulkan pada tumbukan lenting sebagian, koefisien restitusi (e) adalah:

0 < e < 1.

Untuk menentukan koefisien restitusi benda yang bertumbukan, perhatikan contoh berikut ini. Perhatikan gamba berikut!

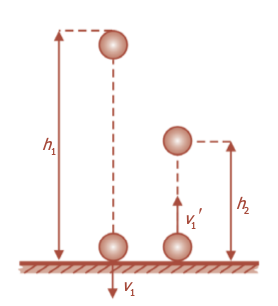
Tumbukan lenting sebagian antara bola dengan lantai.

Sebuah bola elastis jatuh bebas dari ketinggian h₁ dari lantai, maka akan terjadi tumbukan antara bola dengan lantai sehingga bola memantul setinggi h₂. Berdasarkan persamaan pada gerak jatuh bebas, kecepatan benda sesaat sebelum tumbukan adalah:

Gerak bola sesaat setelah terjadi tumbukan dapat diidentifikasikan dengan gerak jatuh bebas, sehingga:

(arah ke atas negatif)

Karena lantai diam, maka kecepatan lantai sebelum dan sesudah tumbukan adalah nol, v₂ = v₂ ' = 0, sehingga besarnya koefisien restitusi adalah:

 (6)

 

3. Tumbukan tidak Lenting Sama Sekali

Pada tumbukan tidak lenting sama sekali, sesudah tumbukan kedua benda bersatu, sehingga kecepatan kedua benda sesudah tumbukan besarnya sama, yaitu v₁' = v₂' = v'. Berdasarkan Hukum Kekekalan Momentum maka:

m₁ v ₁ + m ₂ v₂ = m₁ v₁' + m₂ v₂'

m₁ v₁ + m₂ v₂ = (m₁ + m ₂ ) v'

Karena v₁' = v₂' , maka v₁' – v₂' = 0, sehingga koefisien restitusi (e) adalah:

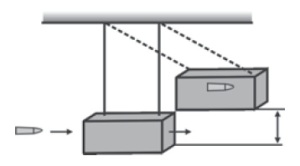Skema Ayunan Balistik

Jadi, pada tumbukan tidak lenting sama sekali besarnya koefisien restitusi adalah nol (e =0).

 

https://sainsmini.blogspot.co.id/2015/12/penjelasan-tentang-tumbukan-lenting.html